深度学习与计算机视觉 体系整理

深度学习与计算机视觉-从人类到机器

2 人工神经元

Posted by 魔峥 on July 13, 2019

人工神经元

前文说过，我们有一个最终目的：设计出一个机器（或数学模型）仿照大脑，使机器具有类似人脑的“学习能力”。20世纪初是仿生学的黄金年代，人们通过研究蝙蝠的避障，海豚的游行研制出雷达和潜水艇。这种思路可以带到人工智能里，通过研究人脑神经的原理，设计出具有人工智能的机器。1943年，心理学家Warren McCulloch和数理逻辑学家Walter Pitts在合作的《A logical calculus of the ideas immanent in nervous activity》论文中提出并给出了人工神经网络的概念及人工神经元的数学模型，从而开创了人工神经网络研究的时代。 1957年，就职于Cornell航空实验室(Cornell Aeronautical Laboratory)的Frank Rosenblatt基于前人的理论，发明了一种最简单形式的前馈式人工神经网络，即“Rosenblatt感知机”。它可以被视为人工神经网络的开端。

1 从神经元到感知机

学过高中生物课程的人一定都记得这张图。

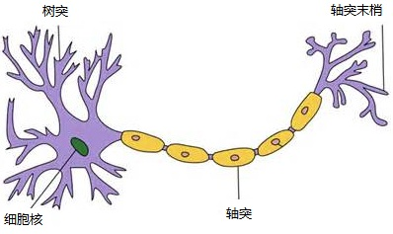
这就是神经元细胞的结构。一端接收数据，一端传输数据。多个神经元组合在一起，下一个神经元接收到信息，如果接收到的递质信号量足够大，可以引起刺激，信号才会向下传递。神经信号，传输过程如下面的图

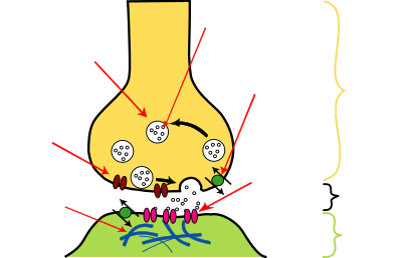
我们可以仿照神经元机制，制造一个这样的神经元：人工神经元一端接收数据一端传输数据，多个人工神经元可以组合在一起，当下一个神经元接收到的信号大于某一个阙值θ时，正向的y才能输出。下图就是根据这样的思想发明出来的M-P模型。 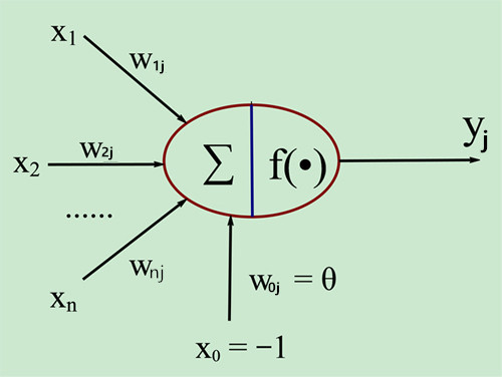\(y_i = f(\sum\limits_{i=1}^n w_{ij}x_i-\theta)\)

这里f(.)是激活函数。使用这个人工神经元的方法很简单，我们将大量的例子“喂”给它。让它自我消化，更新出来一系列神经元内部的参数。这个过程就是“机器学习”。此时，单独的一个M-P模型似乎没什么用。但是伴随着感知机的收敛性（Novikoff定理）这个机器学习算法。感知机立刻变得受人追捧起来。感知机收敛算法概述如下。

1.1 感知机收敛算法概述

感知机通过在空间中寻找一个“超平面”的方法做二分类（AB类）：超平面一边是A类，另一边是B类。例如在一幅海天相接的图片里，海平面将海天分隔开来。当我们做海水、天空二分类时，海平线就是那个“超平面”：一边是海水，一边是天空。 设有一线性二元可分数据集，数据集的输出结果非黑即白（用-1与+1表示），且存在一个超平面将这两种完美分开。输入向量x(n)为二元可分子集，对应的y(n)便签{-1,+1}中+1的一方。 参数变量为： \(\begin{equation} \begin{split} &x(n)=[+1,x_1(n),x_2(n)\cdots,x_m(n)]^T:{m+1维输入向量,n为第n次迭代} \\ &w(n)=[b,w_1(n),w_2(n)\cdots,w_m(n)]^T:{m+1维权值向量,n为第n次迭代} \\ &y(n):{实际响应,结果只有-1与+1二值}\\ &d(n):{期望相应,结果只有-1与+1二值}\\ &\eta:{学习率，比1小的正常数} \end{split} \end{equation}\)

  1. 开始计算第n次迭代权重值w(n)。如果n=0，初始化第n=0次迭代的权重值，w(0)=0.

  2. 计算实际响应y(n)，其中sgn(.)是符号函数： \(y(n)=sgn[w^T(n)x(n)]\)

  3. 如果分类出错则更新向量值w(n+1)，否则不更新： \(w(n+1)=w(n)+\eta[d(n)-y(n)]x(n)\)

  4. 如果w(n)与w(n+1)的误差在容许范围内，停止计算；否则回到步骤1

这里我们还要证明迭代收敛：在有限步骤内可以使w(n)与w(n+1)相等（这里的数据集是线性可分的）。 思维缜密的朋友发现，上面仅仅说了怎样迭代可以得到那个“超平面”，但是没有证明迭代次数的有限性。倘若迭代是无限的，那么自然不存在“超平面了”。迭代次数有限性的证明就是感知机收敛算法。

1.2 感知机收敛证明

首先假设前提，输入向量x(n)为二元可分子集O，对应的y(n)便签{-1,+1}中+1的一方。

\[\eta[d(n)-y(n)]=1, w(0)=0 \\ \therefore w(n+1)=x(1)+x(2)+\cdots+x(n)\]

当第n次为感知机不能正确分类时，修改此时变量权重，有 \(w^T(n)x(n)<0\)

前提说明结束证明开始，该证明分两段：

  1. 第一段
\[\begin{equation}\begin{split} & 设 \ \exists w_0,\alpha,使得 w_0x(n)>0,且a=\min_{x(n) \in O }w^Tx(n) \\ &\therefore w_0^Tw(n+1) \geqslant n\alpha \\ &\because Cauchy-Schwarz不等式，\|w_0\|^2 \|w(n+1)\|^2 \geqslant \|w_0^Tw(n+1)\|^2\\ &\therefore \|w_0\|^2 \|w(n+1)\|^2 \geqslant n^2\alpha^2 \\ &\therefore \|w(n+1)\|^2 \geqslant \frac{n^2\alpha^2}{\|w_0\|^2} \end{split}\end{equation}\]
  1. 第二段
\[\begin{equation}\begin{split} &\|w(n+1)\|^2 = \|w(n)+x(n)\|^2 = \|w(n)\|^2 + \|x(n)\|^2 + 2\|w(n)\|\|x(n)\| \\ &\because w^T(n)x(n)<0 \\ &\therefore \|w(n+1)\|^2 \leqslant \|w(n)\|^2 + \|x(n)\|^2 \\ &\therefore \|w(n+1)\|^2 - \|w(n)\|^2 \leqslant \|x(n)\|^2 \\ \end{split}\end{equation}\]

看见没？高中数学推到这里就该累加了。

\[\begin{equation} \begin{split} &\therefore \|w(n+1)\|^2 \leqslant \sum\limits_{k=1}^n \|x(k)\|^2 \\ & set: \beta=\max_{x(k) \in O}\|x(k)\|^2 \\ &\therefore \|w(n+1)\|^2 \leqslant n\beta \\ &\therefore \frac{n^2\alpha^2}{\|w_0\|^2} \leqslant \|w(n+1)\|^2 \leqslant n\beta \\ &\therefore n \leqslant \frac{\beta\|w_0\|^2}{\alpha^2} \\ \end{split} \end{equation}\]

所以，我们发现当n的更新次数会停止，迭代次数n是有上限的，该算法会收敛。

由上面的推论可以得到，如果是一个线性可分的数据集，我是可以在有限次更新后将数据集完美分割。从某种意义上讲，这样的结果就是上面说的“超平面”。这条经典的定理解释了“感知机为什么会有效”。“机器学习”发展到今天，一次完整训练可能需要几十台机器几个月的时间，如果没有这条收敛定理，我们可能就没有在混沌中继续训练下去的理由了。

感知机看起来是个简单的模型，不用通篇数学公式与证明，但它的发展并不那么顺利。而人工神经元的发展更是一波三折。在相当长的时间里，我们可能只知道支持向量机（SVM）而忘了人工神经元。直到经历过三次危机之后。

2 从单层神经网络到深度学习

2.1 第一次危机：单层感知机不能解决“异或”逻辑问题

之前我一直强调“线性可分数据集”。其实我特意忽视了一点：数据集不可分怎么办？如果两类有交杂部分，且越往外面两类区分越明显。我们可以使用“损失函数”这一概念。定义一个误分类损失函数，然后我们最小化这个损失函数。这就是战争中常说的“尽可能将伤害损失控制到最小”。 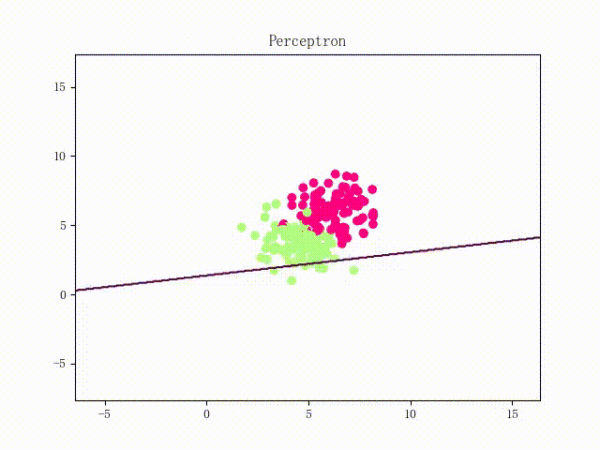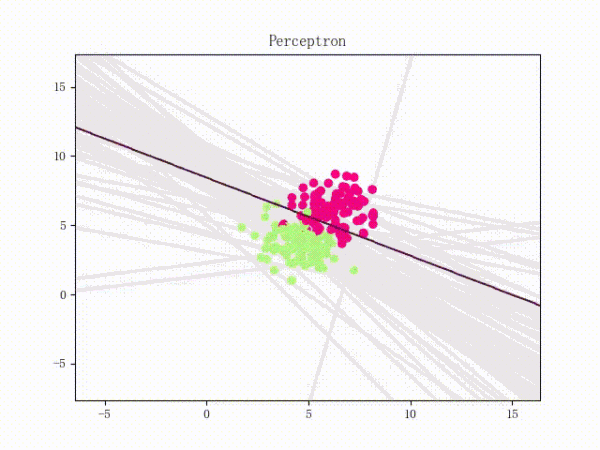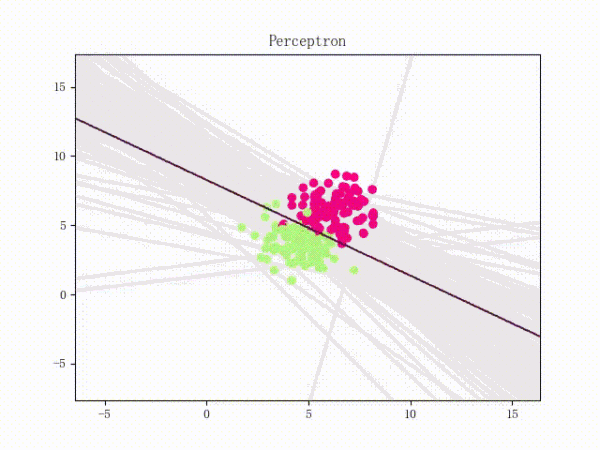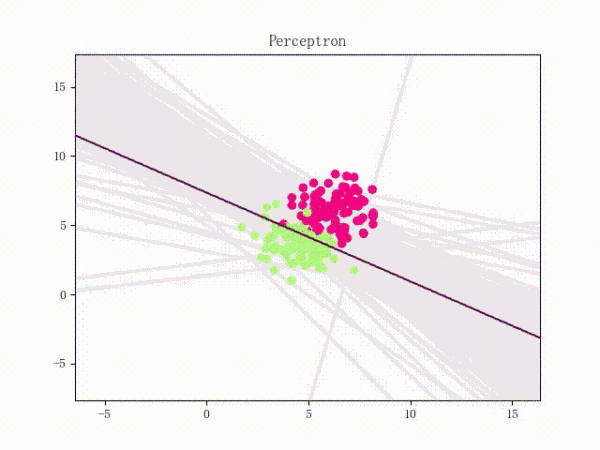但是有一种很简单的小东西比较恶心，那就是简单的异或问题。。如图 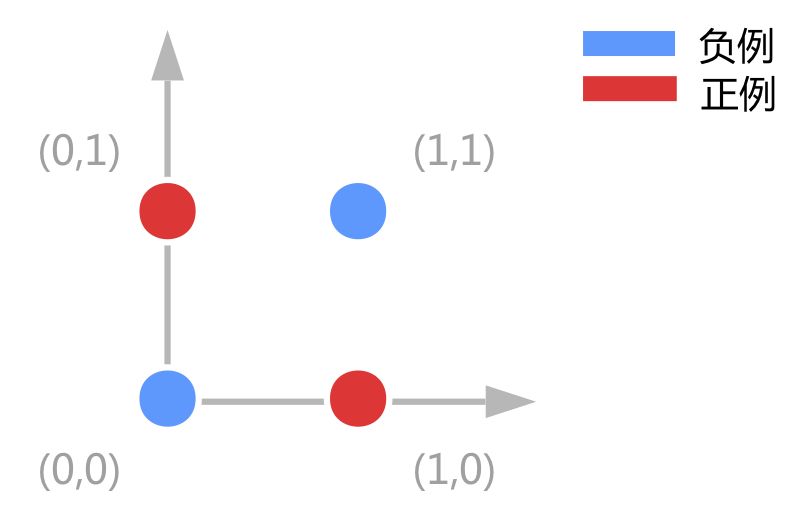我们真的不能画一条线看起来比较好的线来分割。而且这不仅仅是感知机一家的问题， 所有的线性分类器都有这样的问题，包括LDA(Linear discriminant analysis), linear-SVM， Logistic regression都不能做XOR。数学理论是严谨的，但使用数学工具的人是灵活的。我们又发现，具有一个隐藏层组织的神经网络可以解决异或这个问题。我们计算一下: 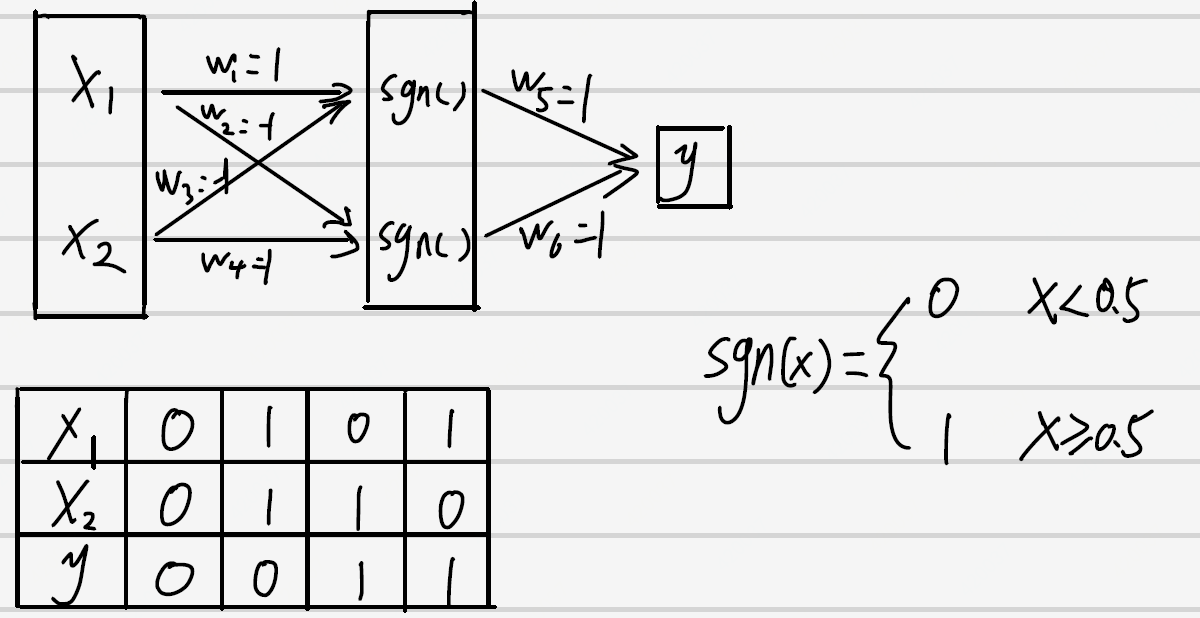这里的sgn后来演化成激活函数。多层的神经元将感知机的研究直接拉入多层人工神经网络时代。

2.2 第二次危机：多层人工神经网络问题

“异或”问题似乎解决了。但却暴露了很大的问题？

  1. 是否还存在一些场景，令多层人工神经网络不适用？
  2. 多层人工神经网络怎么进行参数训练？

第二个问题很快就解决了。1974年Paul Werbos于博士论文中提出BP算法初步解决了多层神经网络的训练问题，1985年由Rumelhart等人发展了该理论。BP算法比较复杂，总结起来就是前向计算，反向求导。 而第一个问题却迟迟不能解决，直到1989年通用近似定理（universal approximation theorrm）(Hornik et al., 1989;Cybenko, 1989) 的发表。在这个定理表明：“一个包含足够隐含层神经元的多层前馈网络，能以任意精度逼近任意预定的连续函数。” 这个定理的原文太复杂，这里可以谈下里面的关键点：

  1. 我们可以设计一个网络，“以任意精度逼近”而不是准确计算。增加隐含层可以提升近似精度。
  2. 被近似的函数必须是连续的。如果是非连续的就爱莫能助了。例如这个函数 \(f(x)=\left\{ \begin{aligned} -1 \ &(x是无理数) \\ 1 \ &(x是有理数) \end{aligned} \right.\)

神经网络往深度层次发展的方向已经有了理论基础。同时该理论又被发展为：三层神经网络（带有隐层）可以以任意精度逼近任意预定的连续函数。这条定理也给出了神经网络可以往广度发展的答案。但不管怎么讲，当时进入“多层人工神经网络时代”的前置数学理论已经建成。但实际情况却不这样，从1989年到2014年，一直拖了25年。主要原因是遭遇了”人工神经网络”的第三次危机：多层人工神经网络计算量爆炸问题。

2.3 第三次危机：多层人工神经网络计算量爆炸问题

神经网络的第三次危机源于计算机算力不足。“通用近似原理”需要叠加神经元层数，BP算法里面有大量求导操作，使得二十世纪九十年代的计算机不堪承受如此的重载。很快人工神经网络的发展再次陷入低潮，一直没被重视。直到2014年Hinton和他的学生Alex Krizhevsky发表AlexNet。不管从是算法的简洁度，结果的准确度都完胜第二名。也是在那年之后，更多的更深的神经网路被提出，比如优秀的VGG，GoogLeNet。AlexNet的最大贡献便是卷积神经网络(Convolutional Neural Networks, CNN)的提出。

  1. CNN改进了以往神经网络连接的方法，将全连接方法为主改为更适合图片的卷积连接方法为主。这种改动大大地减少了运算量。
  2. NVIDIA（英伟达）之前就有图像模板的优化计算，而CNN的本质就是一系列模板卷积的运算，AlexNet利用了这一点，使用多块NVIDIA显卡对大量的卷积计算进行加速。

当然了，全球游戏高端玩家，比特币矿机，AMD的追赶，间接推进NVIDIA进行高并行GPU的快速升级。事实上，“计算爆炸问题”依然没有被消除，而是被“计算机运算能力加强”与“全连接模型简化”两个因素减缓了。但是，就是这一点点减缓，却促使机器学习的精度上了一个台阶。在1943年沃伦·麦克洛克（Warren McCulloch）开创M-P神经元模型的71年后，Hinton和他的学生Alex Krizhevsky带着AlexNet重回人们的视线，带领人类进入“深度学习时代“。

雄关漫道真如铁，而今迈步从头越

CATALOG
    FEATURED TAGS
    深度学习与计算机视觉 体系整理
    FRIENDS